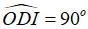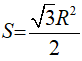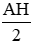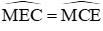Chuyên đề dấu hiệu nhận biết tiếp tuyến của đường tròn

Chuyên đề Dấu hiệu nhận biết tiếp tuyến của đường tròn – Toán 9

A. Lý thuyết

1. Tính chất của tiếp tuyến

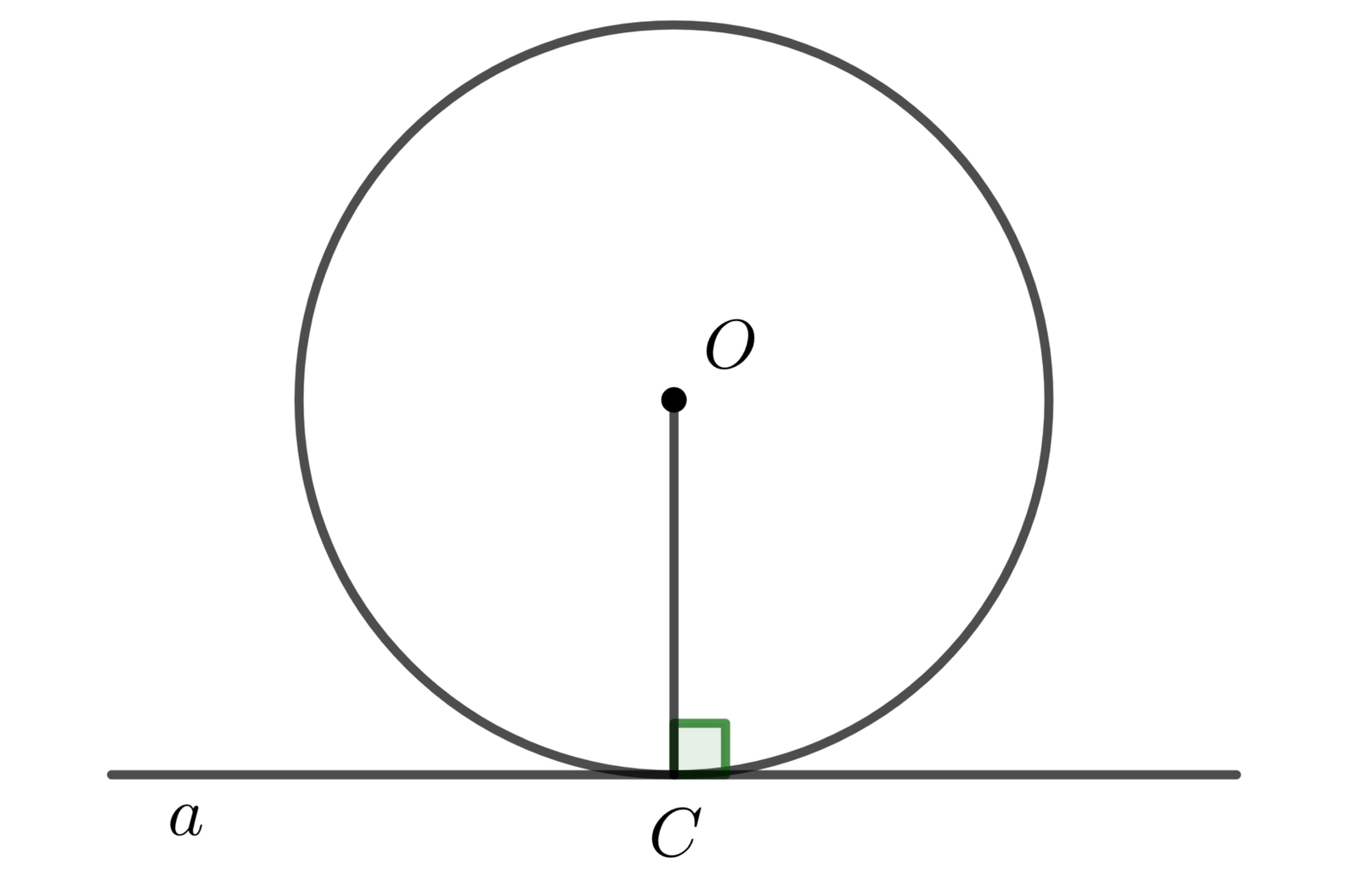
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

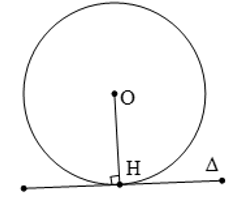
Trong hình vẽ Δ là tiếp tuyến ⇒ Δ ⊥ OH (H là tiếp điểm).

2. Dấu hiệu nhận biết tiếp tuyến của đường tròn.

Để nhận biết một đường thẳng là tiếp tuyến của một đường tròn ta có hai dấu hiệu sau:

    + Dấu hiệu 1: Đường thẳng và đường tròn chỉ có một điểm chung (định nghĩa tiếp tuyến).

    + Dấu hiệu 2: Đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó.

Cụ thể bằng các hiểu sau:

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1: Cho (O; R).Đường thẳng d là tiếp tuyến của đường tròn (O; R) tại tiếp điểm A khi

A. d ⊥ OA tại A và A ∈ (O)

B. d ⊥ OA

C. A ∈ (O)

D. d // OALời giải:

Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn

Chọn đáp án A

Câu 2: Cho (O; 5cm). Đường thẳng d là tiếp tuyến của đường tròn (O; 5cm), khi đó

A. Khoảng cách từ O đến đường thẳng d nhỏ hơn 5cm

B. Khoảng cách từ O đến đường thẳng d lớn hơn 5cm

C. Khoảng cách từ O đến đường thẳng d bằng 5cm

D. Khoảng cách từ đến O đường thẳng d bằng 6cmLời giải:

Khoảng cách từ tâm của một đường tròn đến tiếp tuyến bằng bán kính của đường tròn đó

Chọn đáp án C

Câu 3: Cho tam giác ABC có AC = 3cm, AB = 4cm, BC = 5cm. Vẽ đường tròn (C; CA). Khẳng định nào sau đây là đúng?

A.Đường thẳng BC cắt đường tròn (C; CA) tại một điểm

B.AB là cát tuyến của đường tròn (C; CA)

C.AB là tiếp tuyến của (C; CA)

D. BC là tiếp tuyến của (C; CA)Lời giải:

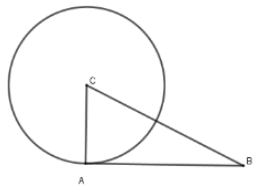
+ Xét tam giác có:

BC2 = 52 = 25; AB2 + AC2 = 42 + 32 = 25 ⇒ BC2 = AB2 + AC2

⇒ ΔABC vuông tại A (Định lý Pytago đảo)

⇒ AB ⊥ AC mà A ∈ (C; CA) nên AB là tiếp tuyến của (C; CA)

Chọn đáp án C

Câu 4: Cho tam giác cân ABC tại A; đường cao AH và BK cắt nhau tại I. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính AI

A. HK

B. IB

C. IC

D. AcLời giải:

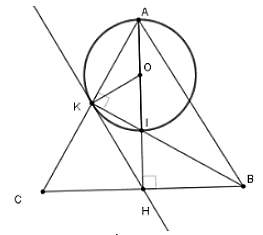
Gọi O là trung điểm AI. Xét tam giác vuông AIK có

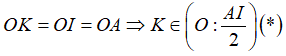
Từ (*) và (**) thì HK là tiếp tuyến của đường tròn đường kính AI

Chọn đáp án A

Câu 5: Cho tam giác vuông ABC tại A, đường cao AH. Đường tròn đường kính BH cắt AB tại D, đường tròn đường kính CH cắt AC tại E. Chọn khẳng định sai trong các khẳng định sau

A. DE là cát tuyến của đường tròn đường kính BH

B. DE là tiếp tuyến của đường tròn đường kính BH

C. Tứ giác AEHD là hình chữ nhật

D. DE ⊥ DI (với I là trung điểm BH)Lời giải:

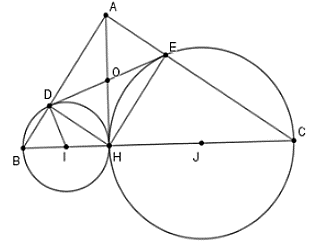
Gọi I, J lần lượt là trung điểm của BH và CH.

Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chứng minh ID ⊥ DE hay 

Vì D, E lần lượt thuộc đường tròn đường kính BH và HC

Nên DE là tiếp tuyến của đường tròn đường kính BH

Từ chứng minh trên suy ra các phương án B, C, D đúng

Chọn đáp án A

Câu 6: Trên tiếp tuyến tại điểm A của đường tròn (O; R) lấy điểm M sao cho OM = 2R. Gọi điểm B của đường tròn (O; R) sao cho MB = MA. Tìm khẳng định sai?

A. MB là tiếp tuyến của đường tròn (O; R).

B. Tam giác ABC là tam giác đều.

C. Diện tích tam giác AOM là: 

D. MA = R√2Lời giải:

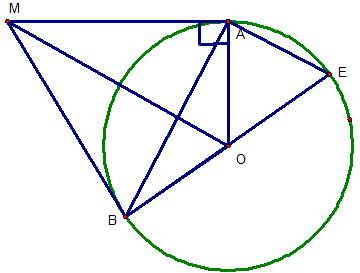
Chọn đáp án D.

Câu 7: Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Tìm khẳng định đúng

A. AC là tiếp tuyến của (B; BA).

B. AB là tiếp tuyến của (A; AC).

C. BC là tiếp tuyến của (A; AC).

D. BC là tiếp tuyến của (A; AB).Lời giải:

Tam giác ABC có: AB2 + AC2 = BC2 nên tam giác BAC vuông tại A.

Ta có: AB ⊥ AC tại A và A thuộc đường tròn (B; BA).

Suy ra: AC là tiếp tuyến của (B; BA).

Chọn đáp án A.

Câu 8: Cho (O; 5cm) có dây AB = 8cm . Qua O , kẻ đường vuông góc với AB cắt tiếp tuyến tại A của đường tròn tại C.

A. BC là tiếp tuyến của (O).

B. Khoảng cách từ O đến AB là 3 cm.

C. OC = 25/3 cm

D. A hoặc B saiLời giải:

Gọi H là giao điểm của AB và CO.

Xét tam giác OAB có OA = OB = R nên tam giác OAB cân tại O.

Lại có, OH là đường cao nên đồng thời là đường phân giác

* Áp dụng hệ thức về cạnh và góc trong tam giác vuông ta có:

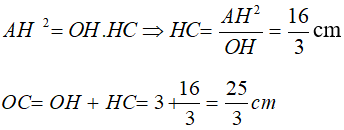
Chọn đáp án D.

Câu 9: Cho hình vuông ABCD. Gọi O là tâm đường tròn đi qua 4 điểm A,B, C, D. Tìm khẳng định đúng?

A. AB là tiếp tuyến của (O).

B. BC là tiếp tuyến của (O).

C.CD là tiếp tuyến của (O)

D. Tất cả saiLời giải:

* Gọi O là giao điểm của hai đường chéo AC và BD

Theo tính chất hình chữ nhật ta có:

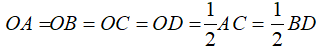
Nên O là tâm đường tròn đi qua 4 điểm A,B, C, D.

Các đường thẳng AB; BC; CD; DA đều có 2 điểm chung với (O) nên 4 đường thẳng này không thể là tiếp tuyến của đường tròn (O)

Chọn đáp án D.

Câu 10: Cho hình vuông ABCD cạnh a, gọi O là tâm đường tròn nội tiếp hình vuông. Tìm khẳng định đúng?

A. AB, BC, CD và DA là các tiếp tuyến của đường tròn (O).

B. AB, BC, CD và DA đều không là tiếp tuyến của đường tròn (O).

C. AC và BD là tiếp tuyến của (O).

D. Tất cả sai.Lời giải:

Gọi O là giao điểm của AC và BD. Khi đó, đường tròn tâm O bán kính R = a/2 là đường tròn nội tiếp hình vuông ABCD.

Do O là tâm đường tròn nội tiếp hình vuông ABCD nên đường tròn tiếp xúc với các cạnh của hình vuông.

Suy ra: AB; BC; CD và DA là các tiếp tuyến của đường tròn (O).

Chọn đáp án A.

II. Bài tập tự luận có lời giải

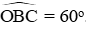
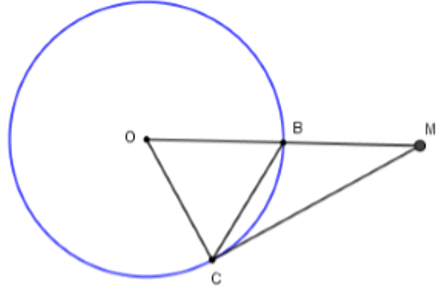
Câu 1: Cho đường tròn (O; 2cm) bán kính OB. Vẽ dây BC sao cho . Trên tia OB lấy điểm M sao cho BM = 2cmLời giải:

Tam giác OBC cân tại O có 

Nên tam giác OCB là tam giác đều suy ra BC = OB = OC = 2

Xét tam giác OCM có BC = OB = BM = 2 = 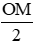 nên ΔOCM vuông tại C

⇒ OC ⊥ CM ⇒ MC là tiếp tuyến của (O; 2cm)

Câu 2: Từ một điểm A ở bên ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với (O). Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC cắt tia AB tại M. Tứ giác AMON là hình gì?

Lời giải:

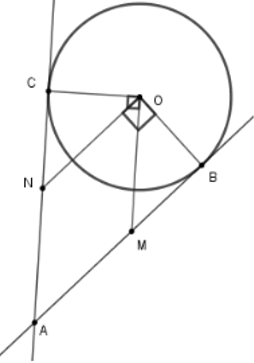
Dễ có AMON là hình bình hành (ON // AM; OM // AN)

Ta chứng minh OM = ON

Câu 3: Cho tam giác ABC có hai đường cao BD, CE cắt nhau tại H. Xác định tâm F của đường tròn đi qua bốn điểm A, D, H, E.Lời giải:

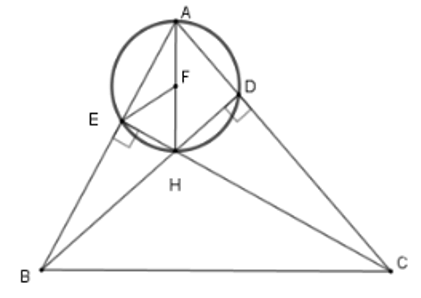
Gọi F là trung điểm của AH

Xét hai tam giác vuông AEH và ADH ta có FA = FH = FE = FD = 

Nên bốn đỉnh A, D, H, E cùng thuộc đường tròn tâm F bán kính 

Câu 4: Cho tam giác ABC có hai đường cao BD, CE cắt nhau tại H. Gọi M là trung điểm BC. Đường tròn (F) ở trên nhận các đường thẳng nào dưới đây là tiếp tuyến?

Lời giải:

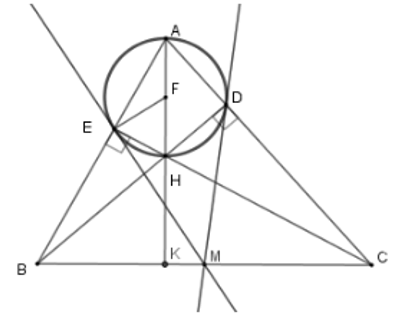
AH cắt BC tại K ⇒ AK ⊥ BC vì H là trực tâm tam giác ABC

Ta chứng minh ME ⊥ EF tại E

∆FAE cân tại F (vì FA = FE) nên:

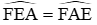
∆MEC cân tại M (vì ME = MC = MB = 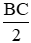) nên 

Từ đó ME là tiếp tuyến của 

Tương tự ta cũng có MD là tiếp tuyến của 

Câu 5: Cho đường tròn (O), dây MN khác đường kính. Qua O kẻ đường vuông góc với MN, cắt tiếp tuyến tại M của đường tròn ở điểm P. Cho bán kính của đường tròn bằng 10cm; MN = 12cm. Tính OP

Lời giải:

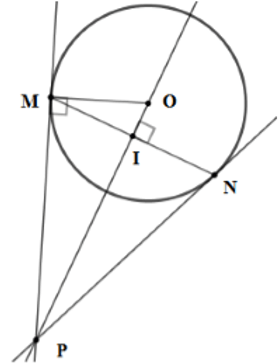
Gọi I là giao điểm của MN và OP

Ta có OP ⊥ MN tại I ⇒ I là trung điểm của MN

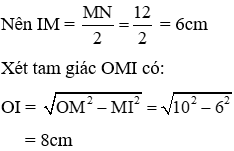
Xét tam giác vuông MPO, theo hệ thức lượng trong tam giác vuông ta có:

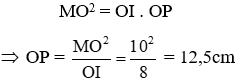
Vậy OP = 12,5cm

Câu 6: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Dùng thước và compa, hãy dựng các điểm B và C thuộc đường tròn (O) sao cho AB và AC là các tiếp tuyến của đường tròn (O).

Lời giải:

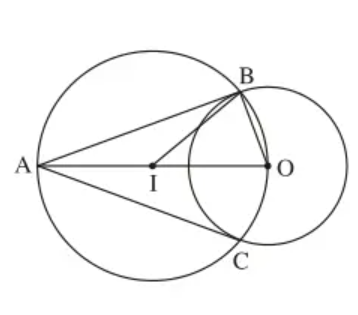
Cách dựng:

– Dựng đoạn thẳng OA và I là trung điểm của OA

– Dựng đường tròn (I; IO) cắt đường tròn (O) tại B và C

– Nối AB, AC ta được hai tiếp tuyến cần dựng

Chứng minh:

Xét tam giác OAB nội tiếp đường tròn (I) có AO là đường kính

Do đó, tam giác OAB vuông tại B

⇒AB⊥BO⇒��⊥��

Do đó, AB là tiếp tuyến của đường tròn (O; OB)

Xét tam giác ACO nội tiếp đường tròn (I) có AO là đường kính

Do đó, tam giác ACO vuông tại C

⇒AC⊥CO⇒��⊥��

Do đó, AC là tiếp tuyến của đường tròn (O; OC) hay đường tròn (O; OB)

Vậy luôn dựng được đường tròn tâm I, cắt đường tròn tâm O tại hai điểm B và C và luôn có AB, AC là hai tiếp tuyến của đường tròn (O).

Câu 7: Cho điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Dựng đường tròn (O) đi qua A và B nhận đường thẳng d làm tiếp tuyến.

Lời giải:

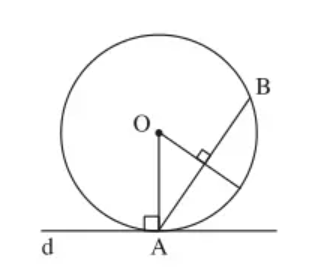
Cách dựng

– Dựng đường thẳng trung trực của AB

– Dựng đường thẳng đi qua A và vuông góc với d. Đường thẳng này cắt đường trung trực của AB tại O

– Dựng đường tròn (O; OA) ta được đường tròn cần dựng

Chứng minh:

Vì O nằm trên đường trung trực của AB nên OA = OB. Khi đó đường tròn (O; OA) đi qua hai điểm A và B

Ta có: OA vuông góc với d tại A nên d là tiếp tuyến của (O)

Vậy (O) thỏa mãn điều kiện bài toán.

Câu 8: Cho tam giác ABC vuông tại A. Vẽ đường tròn (B; BA) và đường tròn (C; CA), chúng cắt nhau tại điểm D (khác A). Chứng minh rằng CD là tiếp tuyến của đường tròn (B).

Lời giải:

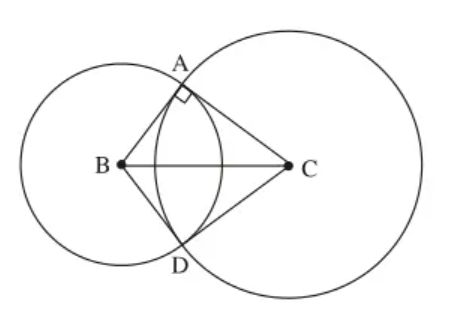
Xét tam giác ABC và tam giác DBC

Có:

BA = BD (bán kính của (B; BA))

CA = CD (bán kính của (C; CA))

BC chung

Do đó, ΔABC = ΔDBC (cạnh – cạnh – cạnh)

⇒ˆBDC=ˆBAC=90o⇒CD⊥DB⇒���^=���^=90�⇒��⊥��

Do đó, CD là tiếp tuyến của đường tròn (B; BA)

Câu 9: Cho góc nhọn xOy, điểm A thuộc tia Ox. Dựng đường tròn tâm I tiếp xúc với Ox tại A và có tâm I nằm trên Oy.

Lời giải:

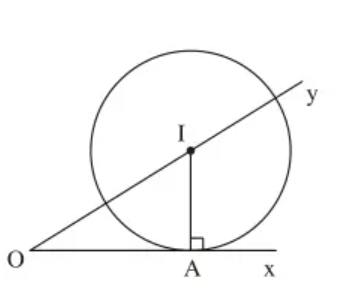
Cách dựng:

– Dựng góc nhọn xOy

– Dựng đường vuông góc với Ox tại A cắt Oy tại I

– Dựng đường tròn (I; IA)

Chứng minh:

Ta có: I nằm trên Oy, OA⊥IA��⊥�� tại A

Do đó, Ox là tiếp tuyến của đường tròn (I; IA) hay (I; IA) tiếp xúc với Ox.

Câu 10: Cho đường tròn (O) và đường thẳng d không giao nhau. Dựng tiếp tuyến của đường tròn (O) sao cho tiếp tuyến đó song song với d.

Lời giải:

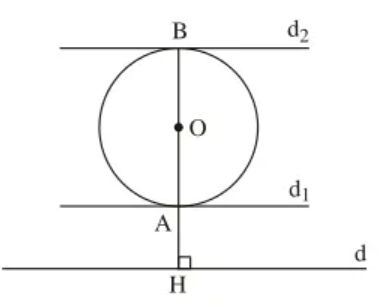
Cách dựng:

– Dựng OH vuông góc với d cắt đường tròn (O) tại A và B

– Dựng đường thẳng d₁ đi qua A và vuông góc với OA

– Dựng đường thẳng d₂ đi qua B và vuông góc với OB

– Khi đó d₁ và d₂ là hai tiếp tuyến cần dựng.

Chứng minh:

Ta có:

A và B thuộc (O) và nằm trên đường thẳng OH

d₁ vuông góc với OA hay d₁ vuông góc với OH tại A

d₂ vuông góc với OB hay d₂ vuông góc với OH tại B

Mà d vuông góc với OH tại H

Do đó, d // d1�1 // d2�2

III. Bài tập vận dụng

Câu 1: Cho đường tròn (O; 12), điểm M cách O 20. Vẽ tiếp tuyến AM với A là tiếp điểm

a) Tính MA

b) Vẽ dây AB vuông góc với OM. Chứng minh MB là tiếp tuyến

Câu 2: Cho đường tròn (O) đường kính AB. C là một điểm trên đường tròn sao cho 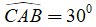. M là điểm đối xứng với O qua B. Chứng minh MC là tiếp tuyến của (O)

Câu 3: Cho tam giác ABC có AB=3, AC=4, BC=5. Vẽ đường tròn (B;BA). Chứng minh rằng AC là tiếp tuyến của đường tròn.

Câu 4: Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A.

Câu 5: Dây cua-roa trên hình 76 có những phần là tiếp tuyến của các đường tròn tâm A, B, C. Chiều quay của đường tròn tâm B ngược chiều quay của kim đồng hồ. Tìm chiều quay của đường tròn tâm A và đường tròn tâm C (cùng chiều quay hay ngược chiều quay của kim đồng hồ).

Câu 6: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Gọi M là trung điểm của AO. Vẽ đường tròn (M ; MO), cắt đường tròn (O) tại B và C. Chứng minh rằng AB và AC là các tiếp tuyến của đường tròn (O).

Câu 7: Cho tam giác cân ABC tại A; đường cao AH và BK cắt nhau tại I. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính AI

Câu 8: Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Vẽ đường tròn (B; BA). Chứng minh rằng AC là tiếp tuyến của đường tròn.

Câu 9: Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A.

Câi 10: Cho tam giác ABC, đường cao AH. Chứng minh rằng đường thẳng BC là tiếp tuyến của đường tròn (A; AH).