Kết nối góc bằng nhau – Toán 9 – Bài 2

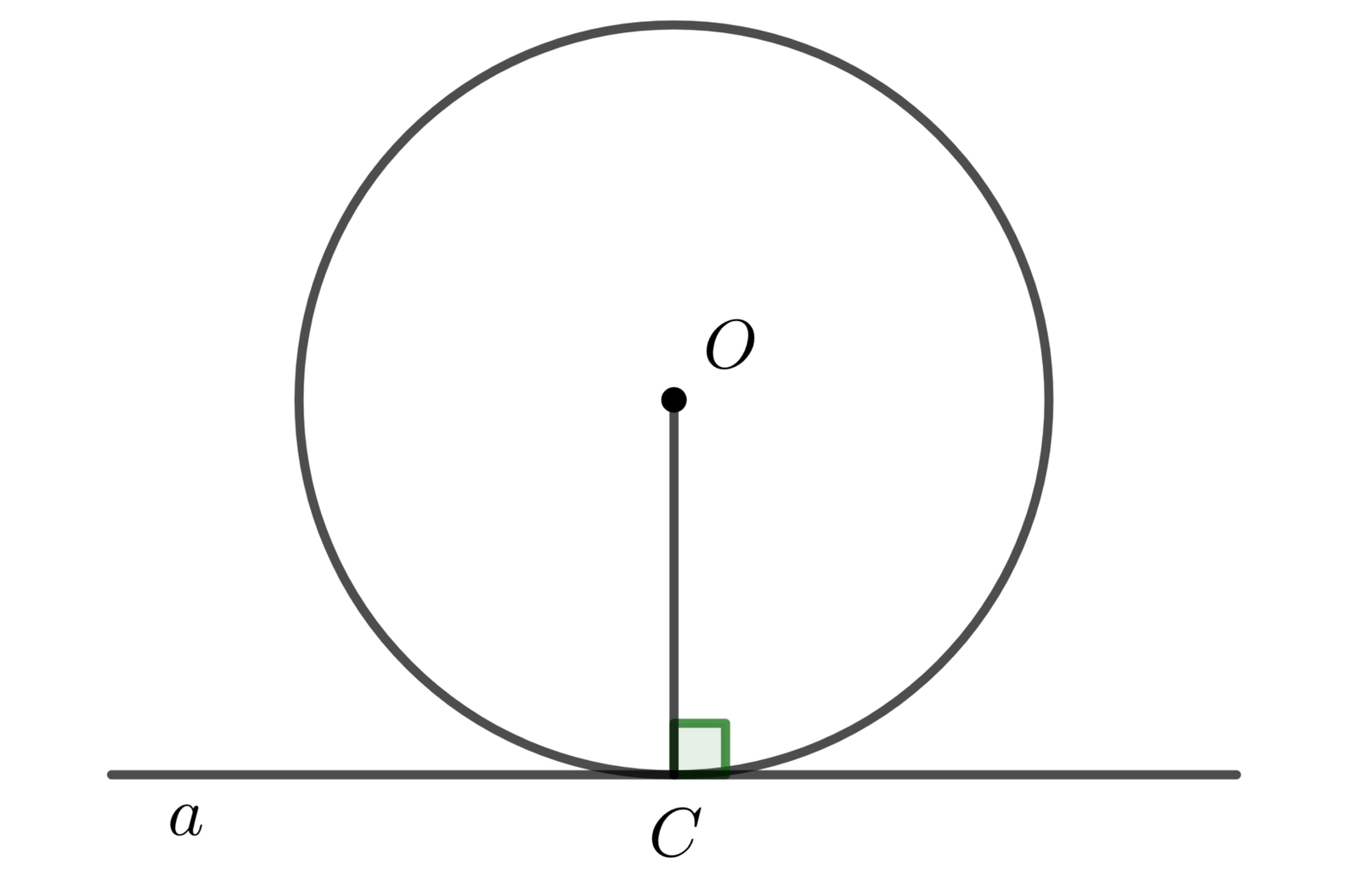
Đề Bài: Cho đường tròn $(\mathrm{O})$. Lấy điểm $\mathrm{A}$ nằm ngoài đường tròn $(\mathrm{O})$, đường thẳng $\mathrm{AO}$ cắt $(\mathrm{O})$ tại hai điểm $B$ và $C$ với $A B<A C$. Qua $A$ vẽ đường thẳng không đi qua $O$ cắt $(O)$ tại hai điểm $D$ và $\mathrm{E}$ với $\mathrm{AD}<\mathrm{AE}$. Đường thẳng vuông góc với $\mathrm{AB}$ tại $\mathrm{A}$ cắt đường thẳng $\mathrm{CE}$ tại $\mathrm{F}$. Gọi $\mathrm{M}$ là giao điểm thứ hai của đường thẳng $FB$ với $(\mathrm{O})$. Tứ giác $AMDF$ là hình gì? Vì sao?