5 năng lực cần đạt trong học Toán & cách rèn luyện hiệu quả
Bài viết dành cho giáo viên, phụ huynh và học sinh muốn chuyển từ “học để làm bài” sang học để hiểu – vận dụng – giải quyết vấn đề với 5 năng lực trọng tâm của môn Toán.
Mục lục
- 5 năng lực toán học là gì?
- Cách rèn từng năng lực: mục tiêu, hoạt động, công cụ, ví dụ bài tập
- Rubric 4 mức đánh giá theo năng lực
- Lộ trình 4 tuần rèn luyện tại lớp & ở nhà
- Câu hỏi thường gặp (FAQ)
1) 5 năng lực toán học là gì?
| Năng lực | Mục tiêu cốt lõi | Kết quả kỳ vọng |
|---|---|---|
| Tư duy & lập luận toán học | Suy luận logic, chứng minh, phản biện | Nói/viết được lý do, phát hiện sai, đưa phản ví dụ |
| Mô hình hoá toán học | Biến vấn đề thực tiễn → mô hình (biểu thức, phương trình, đồ thị…) | Lập mô hình đúng, ước lượng hợp lý, diễn giải kết quả |
| Giải quyết vấn đề | Chọn chiến lược, thử–sai có hệ thống, tổng quát hoá | Tìm nhiều cách giải, biết kiểm tra và tối ưu |
| Giao tiếp toán học | Trình bày, minh hoạ, đặt câu hỏi, hợp tác | Giải thích rõ ràng bằng lời, ký hiệu, hình vẽ, bảng/đồ thị |
| Sử dụng công cụ & phương tiện | Dụng cụ hình học, bảng tính, phần mềm (GeoGebra, Desmos…), máy tính | Dùng công cụ đúng lúc, kiểm chứng kết quả, tăng hiệu suất |
2) Cách rèn từng năng lực
A. Năng lực tư duy & lập luận toán học
Mục tiêu: học sinh biết nêu giả thiết–kết luận, chỉ ra bước suy luận, phân biệt “đúng vì sao/sai ở đâu”.
Hoạt động trên lớp
- Chuỗi “Vì sao?”: với mỗi bước biến đổi, HS phải viết 1 dòng giải thích.
- Săn lỗi: GV đưa lời giải cố ý có lỗi logic; nhóm HS tìm và sửa.
- So sánh hai lời giải: chỉ ra ưu/nhược, bước thừa/thiếu.
Công cụ gợi ý: bảng minh chứng (reasoning map), thẻ “giả thiết–kết luận”, Padlet/OneNote để lưu chuỗi suy luận.
Ví dụ bài tập
Chứng minh: Với mọi số nguyên nn, n2−nn^2 – n là số chẵn.
Yêu cầu HS viết 2 cách lập luận (dựa vào chẵn/lẻ; hoặc nhân tử chung n(n−1)n(n-1)) và nêu lý do ở mỗi bước.
B. Năng lực mô hình hoá toán học
Mục tiêu: xác định biến, tham số; lập biểu thức/đồ thị; ước lượng; kiểm tra tính hợp lý.
Hoạt động trên lớp
- Từ chuyện lớp học → biến & ràng buộc: bán vé sự kiện lớp, tối ưu chi phí in bài, pha dung dịch…
- Bảng 4 bước: (1) Hiểu tình huống → (2) Lập mô hình → (3) Giải mô hình → (4) Diễn giải & kiểm tra.
Công cụ gợi ý: GeoGebra/Desmos (đồ thị), Google Sheets/Excel (bảng giá trị, hồi quy tuyến tính đơn).
Ví dụ bài tập
“Một lớp bán kẹo gây quỹ: giá nhập 6.000đ, bán 10.000đ, chi cố định 150.000đ. Lập mô hình lợi nhuận theo số hộp xx; tìm xx hoà vốn và đề xuất mục tiêu doanh thu.”
C. Năng lực giải quyết vấn đề
Mục tiêu: chọn chiến lược (vẽ hình, xét trường hợp, quy nạp, đặt ẩn phụ…), biết thử–sai thông minh và tổng quát hoá.
Hoạt động trên lớp
- Góc “Chiến lược”: bảng liệt kê 10 chiến lược phổ biến; mỗi khi giải bài, HS đánh dấu chiến lược đã dùng.
- Bài toán mở: “Có bao nhiêu cách?”; “Tìm tất cả giá trị…”; “Thay đổi điều kiện thì kết quả ra sao?”.
Công cụ gợi ý: thẻ chiến lược, nhật ký giải toán (problem-solving journal).
Ví dụ bài tập
“Tìm các cặp số nguyên (x,y)(x,y) thoả x2−y2=84x^2 – y^2 = 84”.
Gợi ý chiến lược: phân tích nhân tử → (x−y)(x+y)=84(x-y)(x+y)=84 → liệt kê ước.
D. Năng lực giao tiếp toán học
Mục tiêu: diễn đạt rõ ràng bằng lời, ký hiệu, hình; đặt câu hỏi, phản biện lịch sự; kể “câu chuyện dữ liệu”.
Hoạt động trên lớp
- 1-2-4-All: cá nhân → cặp → nhóm 4 → cả lớp; mỗi bước phải nói–viết ngắn gọn.
- Áp phích lời giải: nhóm trình bày poster/slide; lớp dùng rubric phản hồi.
Công cụ gợi ý: mẫu poster A3, slide 5–7 trang, Looker Studio cho đồ thị đơn giản.
Ví dụ bài tập
Trình bày cách giải phương trình bậc hai cho bạn chưa học: dùng đồ thị, bảng giá trị và công thức nghiệm; so sánh ưu–nhược từng cách.
E. Năng lực sử dụng công cụ & phương tiện
Mục tiêu: dùng đúng công cụ, hiểu giới hạn công cụ, kiểm chứng chéo bằng cách khác.
Hoạt động trên lớp
- “Hai con đường, một đáp án”: tính diện tích hình phức hợp bằng (1) chia nhỏ – cộng; (2) GeoGebra – phép đo; so sánh sai số.
- Sổ tay công cụ: mỗi em có bảng “khi nào dùng máy tính, khi nào vẽ tay, khi nào dùng bảng tính”.
Công cụ gợi ý: thước–êke–compa, máy tính cầm tay, GeoGebra/Desmos, Google Sheets/Excel, Python (tùy khối).
Ví dụ bài tập
Dùng bảng tính để mô phỏng dãy truy hồi an+1=0.6an+100a_{n+1}=0{.}6a_n + 100 với a0=0a_0=0; nhận xét xu hướng hội tụ và ước lượng giới hạn.
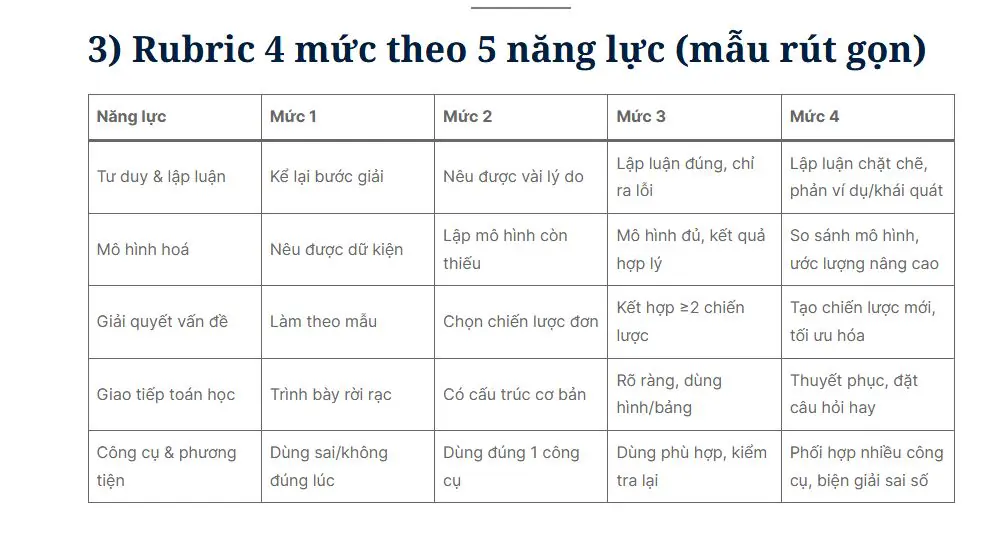
3) Rubric 4 mức theo 5 năng lực (mẫu rút gọn)
| Năng lực | Mức 1 | Mức 2 | Mức 3 | Mức 4 |
|---|---|---|---|---|
| Tư duy & lập luận | Kể lại bước giải | Nêu được vài lý do | Lập luận đúng, chỉ ra lỗi | Lập luận chặt chẽ, phản ví dụ/khái quát |
| Mô hình hoá | Nêu được dữ kiện | Lập mô hình còn thiếu | Mô hình đủ, kết quả hợp lý | So sánh mô hình, ước lượng nâng cao |
| Giải quyết vấn đề | Làm theo mẫu | Chọn chiến lược đơn | Kết hợp ≥2 chiến lược | Tạo chiến lược mới, tối ưu hóa |
| Giao tiếp toán học | Trình bày rời rạc | Có cấu trúc cơ bản | Rõ ràng, dùng hình/bảng | Thuyết phục, đặt câu hỏi hay |
| Công cụ & phương tiện | Dùng sai/không đúng lúc | Dùng đúng 1 công cụ | Dùng phù hợp, kiểm tra lại | Phối hợp nhiều công cụ, biện giải sai số |
Gợi ý chấm điểm: quy đổi 4 mức → thang 10 (2–5–8–10) hoặc dùng trọng số theo chủ đề.
4) Lộ trình 4 tuần rèn luyện (cho 1 chủ đề, ví dụ: Hệ thức lượng tam giác)
Tuần 1 – Hiểu & Lập luận
- Mini-lesson 15’: định nghĩa – tính chất → phiếu “Vì sao?”
- Bài săn lỗi: 3 lời giải sai điển hình.
Tuần 2 – Mô hình hoá & Công cụ
- Tình huống thực tiễn (đo chiều cao cột cờ) → lập mô hình lượng giác.
- GeoGebra: dựng hình, đo góc/độ dài → so sánh sai số.
Tuần 3 – Giải quyết vấn đề
- Bài toán mở: “Tìm cách đo khi không tiếp cận được chân cột”.
- Nhật ký chiến lược: mỗi nhóm ghi 2 chiến lược, so sánh.
Tuần 4 – Giao tiếp & Tổng kết
- Poster/slide 5 trang: “Câu chuyện đo cột cờ của nhóm em”.
- Tự đánh giá bằng Rubric + phản hồi đồng đẳng.
- Bài kiểm tra ngắn: 70% vận dụng – 30% nhớ/hiểu.
Bài tập ở nhà mỗi tuần
- 30–45 phút: 60% bài cơ bản, 40% bài vận dụng; yêu cầu viết lý do với mỗi bước quan trọng.
- Tùy chọn: 1 bài “hai con đường, một đáp án” (giải tay + công cụ).
5) Câu hỏi thường gặp (FAQ)
Hỏi: Rèn đủ 5 năng lực có làm quá tải thời lượng?
Đáp: Không nhất thiết “5 trong mọi tiết”. Mỗi bài nên ưu tiên 1–2 năng lực trọng tâm, các năng lực còn lại xuất hiện ở mức hỗ trợ.
Hỏi: Nếu học sinh yếu, nên bắt đầu từ năng lực nào?
Đáp: Bắt đầu từ giao tiếp (nói–viết ngắn gọn) và tư duy–lập luận mức cơ bản (giải thích một bước). Khi nền tảng vững, thêm mô hình hoá và công cụ.
Hỏi: Có cần công nghệ để rèn năng lực?
Đáp: Nên, nhưng không bắt buộc. Thước–êke–compa + giấy vẫn đủ cho nhiều bài. Công nghệ giúp kiểm chứng nhanh và mở rộng bài toán.




Phản hồi